无论是安培环路定律、磁路中的欧姆定律，还是铁磁材料的磁化曲线和磁滞曲线，都是电生磁过程中的规律和特性。

要说磁场对周遭环境或物体的影响力，还得是法拉第在 1831 年发现的电磁感应定律。

本节就从它说起，然后依次延伸至与它紧密相关的楞次定律和涡流损耗。

电磁感应定律

导体回路中感应电动势的大小，与穿过回路的磁通量变化率成正比。使用公式表示如下：

\[e_{ind} = -\frac{d\phi}{dt}\]

其中，e_ind 是导体回路中产生的感应电动势，φ 是 t 时刻在回路中穿过的磁通量。

在上式中，感应电动势的单位是伏特 (V)，磁通量的单位是韦伯 (Wb)，时间的单位是秒 (s)。

这就是著名的电磁感应定律，也叫做法拉第定律。

如果是一个 N 匝线圈，当线圈中的磁通量变化时，每匝线圈中都会产生感应电动势。由于匝与匝之间是相互串联的，整个线圈中产生的总感应电动势等于各匝线圈中产生的感应电动势之和：

\[\begin{align*} e_{ind} &= \sum_{i=1}^{N}e_i \\ &= \sum_{i=1}^{N} \frac{d (\phi_i)}{dt} &= \frac{d}{dt} \bigg (\sum_{i=1}^{N} \phi_i \bigg) \end{align*}\]

其中，e_i 是第 i 匝线圈中产生的感应电动势，φ_i 是穿过第 i 匝线圈的磁通量。

上式中圆括号中的部分叫做全磁通（或者磁通匝链数），用符号 λ 表示。因此，电磁感应定律也可以表示如下：

\[\begin{align*} e_{ind} &= \frac{d \lambda}{dt} \\ \lambda &= \sum_{i=1}^{N} \phi_i \end{align*}\]

如果线圈匝得很紧，漏磁很少，每一匝线圈中的磁通量大致相同（均为 φ）。那么电磁感应定律可以简化如下：

\[\begin{align*} e_{ind} &= -\frac{d \lambda}{dt} \\ &= -\frac{d(N\phi)}{dt} \\ &= -N\frac{d\phi}{dt} \end{align*}\]

楞次定律

注意到电磁感应定律公式中的负号了吗? 有没有好奇为什么要加这个负号呢?

根据楞次定律，闭合回路中感应电流的方向，总是使得它所激发出的磁场与引起该感应电流的磁通量变化方向相反。电磁感应定律中的负号，其实就是表明感应电动势的方向。

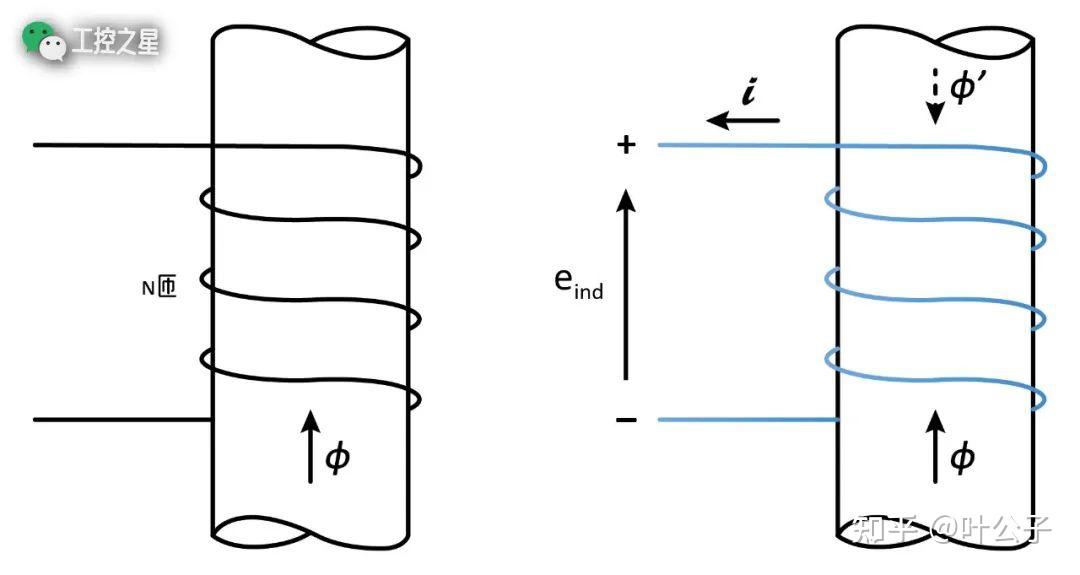
以上图为例，铁芯上缠绕着一个 N 匝线圈，如左图所示。假设铁芯中的磁通量 (φ) 方向向上，且磁场强度正在逐渐增加，

根据电磁感应定律，铁芯中的磁通量变化会让线圈中产生感应电动势。根据楞次定律，该感应电动势产生的感应磁场（φ’）与铁芯中原有磁场（φ）的变化方向相反，即感应磁场的方向应该是向下的。

根据右手定则，要使感应磁场的方向向下，线圈中的感应电流应该是顺时针方向，如右图所示。也就是说，线圈的上端头是感应电动势的正极，下端头是感应电动势的负极。

由于感应电动势的方向可以根据楞次定律判断出来，电磁感应定律公式中的负号经常被省略。

铁芯的涡流损耗

铁芯中的磁通量变化，不只会在线圈中产生感应电动势，也会在铁芯中产生感应电动势。铁芯中的感应电动势，会在铁芯中引起旋涡状电流 —— 涡流。

由于铁芯属于电阻材料，铁芯中的涡流会产生热量散发出去，引起能量损失。这种能量损失，叫做涡流损耗。

涡流损耗的大小，取决于涡流的大小和铁芯的电阻率。涡流越大，说明铁芯中的感应电动势越大。铁芯中的感应电动势越大，感应电流就越大，产生的热量 (I^2^R) 就越多，能量损失就越大。另外，如果涡流中的感应电动势是一定的，铁芯的电阻率越大，感应电流越小，产生的热量就越少，能量损失也就越小。

因此，要减少变压器或电动机中的涡流损耗，最常用的方法有两种：

改用叠片结构的铁芯，以减小涡流。比如，使用叠合在一起的硅钢片代替整块铁芯，各硅钢片之间涂上绝缘漆或其他绝缘材料。叠片结构可以将涡流限制在各个薄片（叠片）内，大幅减小了涡流，从而减少了铁芯的涡流损耗。各叠片之间的绝缘层非常非常薄，几乎不会对铁芯的磁性产生什么影响。

涡流损耗的大小，与铁芯叠片的厚度成正比。因此，铁芯叠片越薄越好。使用叠片铁芯时，叠片要尽可能与磁通量的方向平行。

提高铁芯材料的电阻率。二十世纪以前，铁芯材料以低碳钢为主。由于低碳钢的电阻率低，涡流损耗大。二十世纪末，英国人哈德菲尔特 (R.A.Hadfield) 发现，向钢中添加一定量的硅可以大大提高钢板的电阻率，从而降低涡流损耗。二十世纪以后，硅钢板迅速取代低碳钢，成为了变压器和电机铁芯的主要材料。

这两种减少涡流损耗的方法既可以单独使用，也可以一起使用。如果一起使用，铁芯的涡流损耗将比磁滞损耗小得多得多得多。

参考资料

1. Stephen J. Chapman. Electric Machinery Fundamentals: fifth edition [M]. Australia: McGraw-Hill, 2012: 28-33.
2. 赵凯华, 陈熙谋. 电磁学 [M]. 北京: 高等教育出版社, 2003: 155-162.
3. 宝钢硅钢.（宝钢硅钢）发展历史 [OL].
4. 百度百科. 电工钢（软磁合金） [OL].