上一篇文章演示了一个直线直流电机简易模型的启动过程。启动过程完成后,简易模型进入匀速直线运动状态(平衡状态)。
如果这时向简易模型中的导电棒施加一个与其运动方向相反的外力,会怎么样呢?
简易模型启动完成后
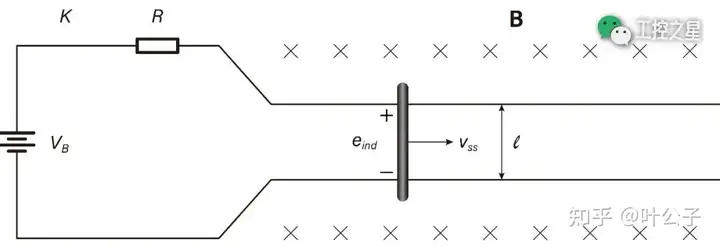
在直线直流电机简易模型中,有一组电池、一个电阻和一对儿绝对光滑的导轨。导轨上平放着一根金属导电棒。导轨的周围分布着均匀的恒磁场,方向垂直于屏幕向里。
电池、电阻、导轨、导电棒和开关组成了一个电路。开关一闭合,简易模型就启动了。
启动过程完成后,导电棒以速度 vss 向右保持匀速直线运动,并由此产生了一个与电源电压大小相同、方向相反的感应电动势 (eind)。这时,导电棒处于平衡状态(受力为零),电路中也没有电流。
\[\begin{align*} v_{ss} &= \frac{V_B}{Bl} \\ e_{ind} &= V_B \\ F_{net} &= F_{ind} = 0 \\ i &= 0 \end{align*}\]外力引起的运动状态变化
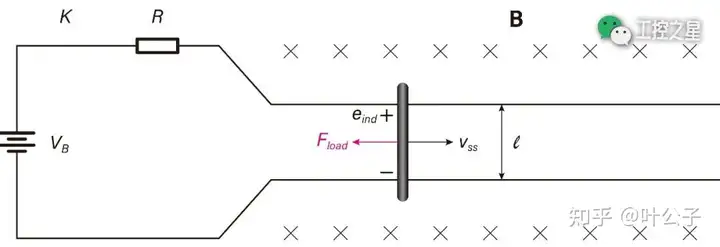
简易模型启动完成后,导电棒突然受到一个水平向左(与其运动方向相反)的外力 (Fload),如图所示。
根据牛顿第二定律,导电棒在外力的作用下将产生水平向左的加速度,从而使移动速度(v)下降。
\[F_{net} = -F_{load} = -ma\]根据感生电动势的计算公式,导电棒的移动速度 (v) 下降了,导电棒上的感应电动势 (eind) 就会随之下降。
\[\overset {\downarrow} e_{ind} = \overset {\downarrow} vBl\]根据基尔霍夫电压定律,导电棒上的感应电动势下降了,电路中的电流就会增大。
\[\begin{align*} \overset {\uparrow} i = \frac{V_B - \overset {\downarrow} e_{ind}}{R} & \end{align*}\]根据安培力的计算公式,电流增大了,磁场向导电棒施加的安培力就会增大。
\[\begin{align} \overset {\uparrow} F_{ind} = \overset {\uparrow} ilB \end{align}\]当导电棒受到的安培力增大到与外力大小相等时,导电棒达到平衡状态,即导电棒又恢复到匀速直线运动状态了。只是,导电棒的运动速度相比之前下降了一些。
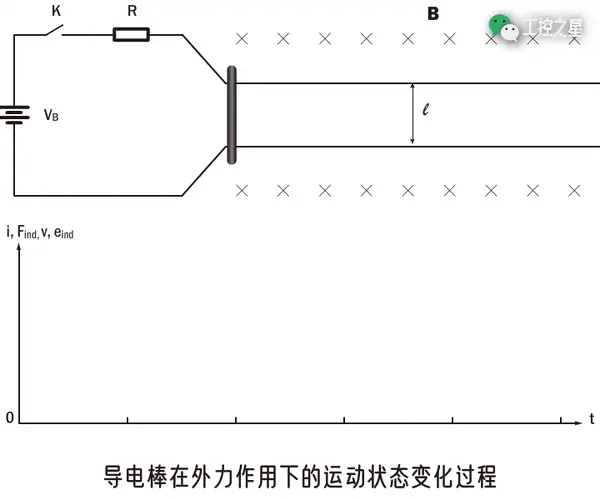
电动机的工作原理
上文中简易模型的运动状态变化过程,其实就是直线直流电动机的工作过程:
当电动机的输出轴上增加了负载之后,输出轴的转速就会下降。输出轴的转速下降了,线圈中的感应电动势就会下降。线圈中的感应电动势下降了,线圈中的电流就会增加。
线圈中的电流增加了,线圈受到的安培力就会增大。线圈受到的安培力增大了,线圈上产生的扭矩也就增大了。
当电动机达到平衡状态时,线圈上产生的扭矩与电动机负载产生的扭矩相等,电动机的输出轴保持匀速转动,但转速比空载时低一些。
如此以来,电动机就实现了从电能到机械能的转换。转换方程如下:
\[P_{conv} = F_{ind}v\]如果以角速度表示的话,转换方程还可以写为:
\[P_{conv} = \tau_{ind}\omega\]其中,τind 是安培力 Find 在旋转运动中的对应物理量,角速度 ω 是速率 v 在旋转运动中的对应物理量。
参考资料
- Stephen J. Chapman. Electric Machinery Fundamentals: fifth edition [M]. Australia: McGraw-Hill, 2012: 39-41.