电机，离不开转动。

电机的转轴，通常是固定的。在物理学中，这样的转动叫做定轴转动。

要精确地描述定轴转动，首先要了解与它相关的三个基本物理量：角坐标、角速度和角加速度。

角坐标

在平面直角坐标系中，横坐标（x）和纵坐标（y）可以唯一确定物体的位置。

对于定轴转动来说，只需要知道转动的角度就可以唯一确定物体的位置了。所以在定轴转动中，转动的角度也称为角坐标（θ）。

角坐标有两种度量方法：弧度制和角度制。其中，弧度是国际单位制导出的单位。

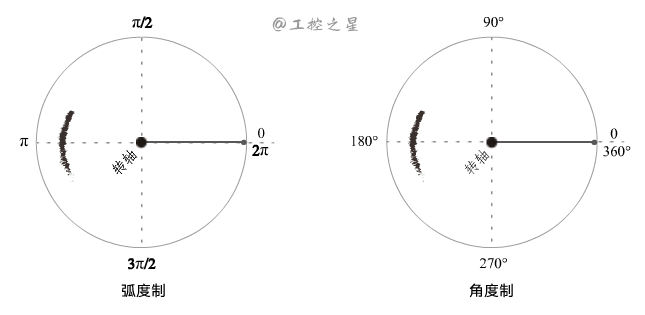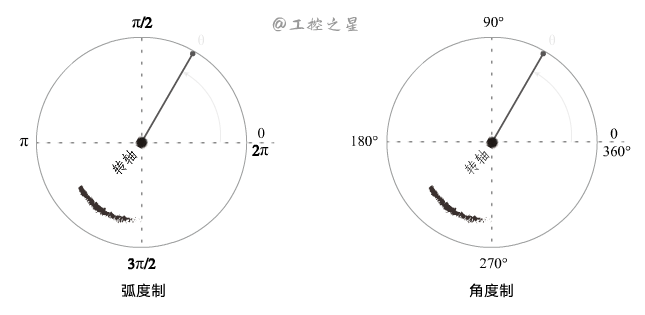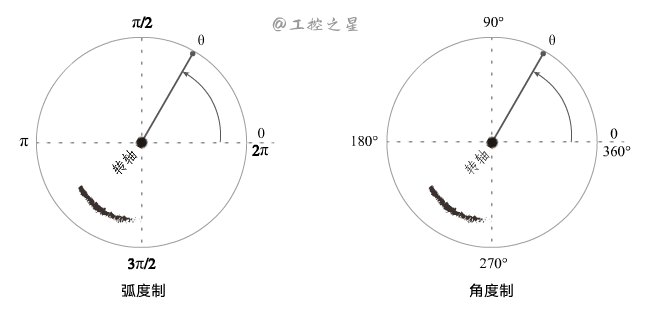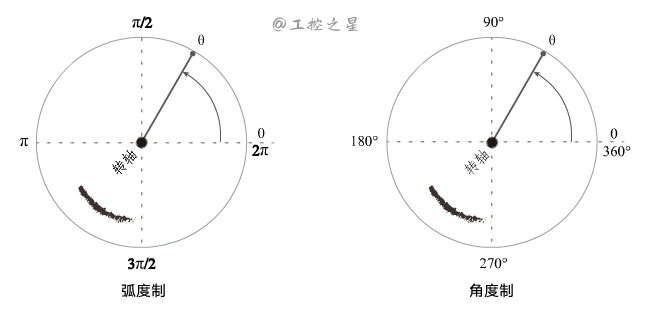
弧度（rad）和角度（°）的换算关系如下：

\[1 rad = \frac{180°}{\pi}\]

角速度

在直线运动中，速度（v）表示物体运动的快慢，其计算公式如下：

\[v = \frac{dr}{dt}\]

其中，r 是物体的位移，t 是物体移动到位经历的时间。

在旋转运动中，角速度（ω）表示物体转动的快慢，其计算公式如下：

\[\omega = \frac{d\theta}{dt}\]

其中，θ 是物体的角位移（转动的角度），t 是物体转动到位经历的时间。

和速度一样，角速度也是矢量。角速度的方向使用右手螺旋法则确定：逆时针方向为正，顺时针方向为负。

在国际单位制中，角速度的单位是弧度/分。除此之外，转/秒和转/分也是角速度的常用单位。

表：角速度的常用单位

单位名称	单位符号
弧度/分	rad/s
转/秒	rps
转/分	rpm

为了最大限度地避免混淆，根据单位的不同，角速度也使用不同的符号表示。

表：角速度符号与角速度单位的对应关系

角速度 符号	角速度 单位
ωm	rad/s
fm	rps
nm	rpm

这三种角速度的换算关系如下：

\[\begin{align*} n_m &= 60f_m \\ f_m &= \frac{\omega_m}{2\pi} \end{align*}\]

角速度符号中的下标 m 表示这是一个力学物理量，以区别于电学物理量。

角加速度

在直线运动中，加速度（a）表示物体转动速度变化的快慢，其计算公式如下：

\[a = \frac{dv}{dt}\]

其中，v 是物体运动的速度，t 是物体速度变化经历的时间。

在旋转运动中，角加速度（α）表示物体转动速度变化的快慢，其计算公式如下：

\[\alpha = \frac{d\omega}{dt}\]

其中，ω 是物体转动的角速度，t 是物体角速度变化经历的时间。

角加速度的度量单位是弧度/秒²（rad/s²）。

注意哦，上式中角速度符号使用的是 ω，说明角速度的单位是弧度/秒。

参考资料

1. Stephen J. Chapman. Electric Machinery Fundamentals: fifth edition. Australia: McGraw-Hill, 2012: 3-4.
2. 赵凯华, 罗蔚茵. 新概念物理教程: 力学. 高等教育出版社, 2004: 171-176.