无论是安培环路定律、磁路中的欧姆定律,还是铁磁材料的磁化曲线和磁滞曲线,都是电生磁过程中的规律和特性。
要说磁场对周围环境或物体的影响力,除了电磁感应定律、安培力和洛伦兹力之外,还有动生电动势。所有发电机的正常运转都离不开动生电动势。
本节将详细说明动生电动势的计算方法,以及判断动生电动势方向的中西手法。
动生电动势
根据电磁感应定律,导体回路中的磁通量变化会产生感应电动势。除此之外,还有一种方法可以产生感应电动势,那就是用“导体切割磁力线”。
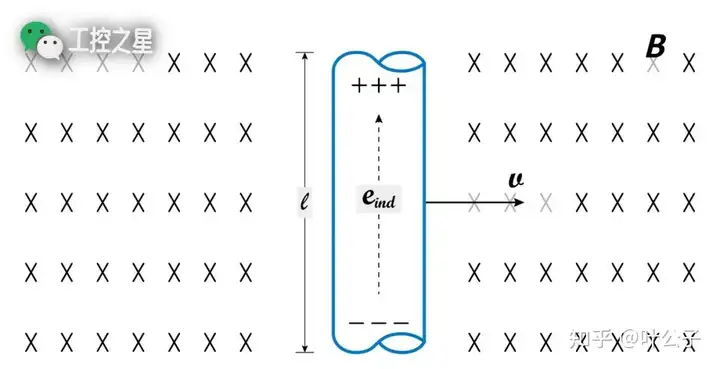
假如磁场中有一段导体,导体的方向与磁场(磁通密度 B)的方向垂直,如图所示。
当导体在磁场中移动时,只要它“切割磁力线”了,导体两端就会产生感应电动势。这种由导体运动产生的感应电动势,叫做动生电动势。
动生电动势的计算方法如下:
\[e_{ind} = \Large (v \normalsize \times \Large B) \cdot \Large l\]其中,v 是导体的运动速度,B 是导体所处磁场的磁通密度,l 是导体的长度。三者均为矢量。
这里需要特别注意的是(敲黑板啦),导体的运动速度 (v) 和磁通密度 (B) 之间是叉乘,其计算结果和导体的长度 (l) 之间是点乘。
叉乘和点乘都是向量之间的运算,但它们是两种不同的运算。
叉乘,又叫向量积,其计算结果也是一个向量。结果向量的大小可计算如下:
\[\vec{a} \times \vec{b} = |\vec{a}| |\vec{b}| \sin \theta\]其中,θ 是两个运算向量 (a 和 b) 之间的夹角,且 θ 的取值范围是 0~180°。
结果向量的方向,垂直于两个运算向量所在平面,是该平面的法向向量。
点乘,又叫数量积,其计算结果是一个标量。它的大小可计算如下:
\[\vec{a} \Large \cdot \normalsize \vec{b} = |\vec{a}| |\vec{b}| \cos \theta\]其中,θ 是两个运算向量 (a 和 b) 之间的夹角,且 θ 的取值范围是 0~180°。
因此,动生电动势的大小可计算如下:
\[\begin{align*} e_{ind} &= \Large (v \normalsize \times \Large B) \cdot \Large l \\ &= vB \sin \theta \cdot l \cos \alpha \\ &= vBl \sin \theta \cos \alpha \end{align*}\]其中,θ 是导体的运动方向 (v) 和磁场方向 (B) 之间的夹角,α 是二者叉乘的结果向量 (v×B) 和导体的长度方向 (l) 之间的夹角。
右手定则
要判断动生电动势的方向,使用右手定则:
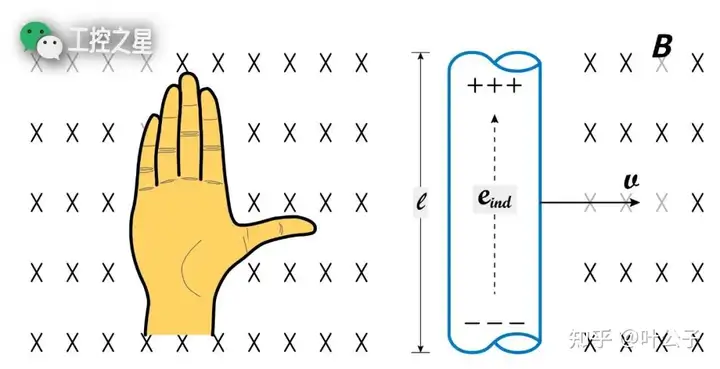
- 伸出右手,摊平手掌。
- 使大姆指与其余四个手指垂直。
- 调整手的方向,使磁感线从掌心垂直进入,并使大姆指指向导体运动的方向。
- 此时,其余四指所指的方向就是动生电动势的方向。
(西式)右手定则一
在判断动生电动势的方向时,国外虽然也使用右手定则,手法却大不相同。而且,此右手定则通常被称为右手定则一,以区别于右手螺旋定则(在国外被称为右手定则二)。
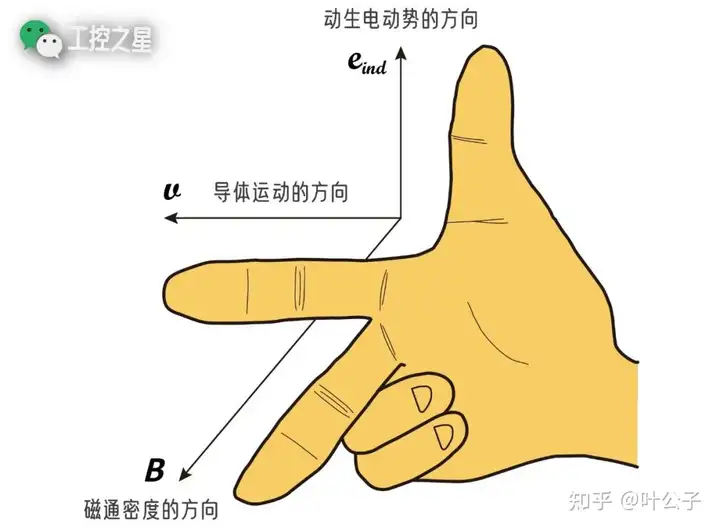
- 伸出右手,摊平手掌。
- 使大姆指与其余四个手指垂直。
- 转动中指使其垂直于手掌,并使无名指和小姆指自然弯曲。
- 调整手的方向,使食指指向导体运动的方向,中指指向磁通密度的方向。
- 此时,大姆指所指的方向就是动生电动势的方向。
右手定则一也可以用来判断安培力的方向。如果结合叉乘的概念,仔细对比一下这两种场景中的手法,你肯定会发现一些规律:
调整手的方向时,食指都是指向第一个运算向量的方向,中指都是指向第二个运算向量的方向,然后大姆指的指向就是结果向量的方向。
可能这个手法中各手指指向的表意不太好记吧,国外还会使用弗莱明左手定则判断安培力的方向,使用弗莱明右手定则判断动生电动势的方向。
弗莱明左手定则和弗莱明右手定则,其实可以看作右手定则一的变种,对各手指指向的表意作了统一,以方便记忆。
感兴趣的小伙伴儿,可以去搜索一下,说不定以后查阅外文资料的时候用得到呢!
参考资料
- Stephen J. Chapman. Electric Machinery Fundamentals: fifth edition [M]. Australia: McGraw-Hill, 2012: 34-36.
- 赵凯华, 陈熙谋. 电磁学[M]. 北京: 高等教育出版社, 2003: 162-164.
- 彭前程, 黄恕伯. (普通高中教科书)物理: 选择性必修 第二册[M]. 北京: 人民教育出版社,2019: 28.
- BYJU’S. Fleming’s Left-Hand Rule and Fleming’s Right-Hand Rule [OL]. (2023-05-05)[2023-11-01].